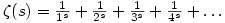หากเอ่ยถึงประเทศเบลเยียม คงเป็นแดนสวรรค์แห่งผู้ที่หลงใหลช็อกโกแลตเป็นอย่างมาก เพราะทั้งประเทศไม่ว่าจะเดินไปตามตรอกซอกซอยไหน เป็นอันต้องเจอะกับร้านขายช็อกโกแลตที่หน้าตาสวยงามชวนน้ำลายย้อย เนื่องจากประเทศเบลเยียมนั้นเลื่องชื่อในด้านของการผลิตช็อกโกแลตรสเลิศ แถมรูปลักษณ์นั้นสุดแสนจะน่าหม่ำ ไม่ใช่มีเพียงช็อคโกแลตเท่านั้นที่ดูน่าตื่นตาตื่นใจยังมีอะไรๆที่เรายังไม่รู้อีกนะคะ อยากรู้แล้วใช่ม๊า ไปดูกันเลย
ท่องโลกไปด้วยกันและค้นพบความมหัศจรรย์แห่งโลกในมุมมองที่ไม่เคยเห็น กับสิ่งที่ซ่อนอยู่
วันศุกร์ที่ 3 ตุลาคม พ.ศ. 2557
วันอังคารที่ 23 กันยายน พ.ศ. 2557
มหัศจรรย์ เม็ดทราย เมื่อขยายด้วยกล้องจุลทรรศ์ 250 เท่า
แปลกแต่จริง บอกฉันสิว่าทุกอย่างไม่ใช่ฝัน บอกกับฉันว่าเธอทำได้ยังไง อิอิ มาเป็นบทเพลงกันเลยทีเดียว สำหรับบทความนี้เป็นเพียงบทความสั้นๆแต่น่าสนใจมากค่ะ สิ่งรอบตัวเราที่คาดไม่ถึงว่าจะมีอะไรมากกว่าที่คิดจะสวยงามและแปลกขนาดนี้กับเม็ดทรายตามชายทะเลนี่แหละค่ะ จะสวยแค่ใหน Here we Go!!
ในความคิดเห็นส่วนตัวนะคะคิดว่านี่ไม่ใช่เม็ดทรายไปทั้งหมดหรอกค่ะ เม็ดทรายจริงๆแล้วเป็นแร่ Quartz Feldspar rock fragment and mica etc อันนี้น่าจะเป็นส่วนของเปลือกหอยไม่ก็สิ่งมีชีวิตเล็กๆที่ผสมๆรวมกับเม็ดทรายมากกว่านะคะ ^^ แต่ก็สวยมากจริงๆค่ะ ว่างๆคงต้องไปนั่งดูบ้าง555
ขอบคุณเว็บไซน์ : http://www.dek-d.com/board/view/3380584/
วันเสาร์ที่ 20 กันยายน พ.ศ. 2557
10 หลุมอุกกาบาต ที่มีบนโลกจริงๆ
...นอกโลกมีหลายอย่างที่ยังไม่เคยเห็นด้วยตาของตัวเอง แต่ก็มีปรากฎการณ์ทางธรรมชาติหลายๆอย่างที่เกิดขี้นจากนอกโลกจนเราต้องรู้สึกตลึง บางครั้งก็สวยจนตลึง แต่บางครั้งก็น่ากลัวจนตลึงเหมือนกับ"หลุมอุกกาบาต"ที่จะเอามาให้ได้ยลโฉมกับความใหญ่ของมัน
ลองจินตนาการว่าวันหนึ่งคุณกำลังแหงนหน้า มองท้องฟ้าโปร่งยามราตรี ทันใดนั้นสายตาคุณก็ไปสะดุดเข้ากับจุดสีเหลืองเล็กๆ ที่ปลายขอบฟ้า พอลองดูดีๆ กลับพบว่าไอ้จุดที่ว่านั้นมีขนาดใหญ่กว่าบ้านคุณไม่รู้กี่เท่า แถมยังพุ่งเข้ามาเรื่อยๆ อีกต่างหาก
ใช่แล้วครับ จุดสีเหลืองที่ว่านั้นก็คืออุกกาบาตจากนอกโลกนั่นเอง วัตถุมหึมาที่เคลื่อนที่ด้วยความเร็วเหนือเสียงนี้ ก่อหายนะมหาศาลอย่างคาดไม่ถึง ทั้งสึนามิหรือแผ่นดินไหว ฝุ่นควันที่เกิดจากการชนโลกสามารถบดบังแสงจากดวงอาทิตย์ได้เป็นปีๆ
สิ่งเหล่านี้เคยเกิดขึ้นกับโลกเรามาแล้วนับครั้งไม่ถ้วนครับ ก่อนที่เราจะกังวลกับเรื่องดาวตกมากกว่านี้ เปลี่ยนบรรยากาศมาชมภาพหลุมอุกกาบาตที่ยิ่งใหญ่ที่สุด 10 แห่งของโลกกันดีกว่า
10.Chicxulub Crater, Mexico
หลุมนี้เกิดขึ้นจากการชนของอุกกาบาตขนาดยักษ์เมื่อ 65 ล้านปีก่อน ก่อให้เกิดแรงระเบิดที่เทียบเท่ากับระเบิด TNT 100 เทราตัน คาดกันว่าเพราะการชนครั้งนี้ทำให้ไดโนเสาร์สูญพันธุ์จนหมดสิ้น เพราะแรงระเบิดของมันก่อให้เกิดสึนามิ แผ่นดินไหว และเกิดการระเบิดของภูเขาไฟ โลกทั้งใบถูกปกคลุมด้วยฝุ่นควันมหาศาลจนสิ่งมีชีวิตส่วนใหญ่ไม่สามารถดำรงชีวิตอยู่ได้
9.Manicouagan Crater, Canada
มีอีกชื่อหนึ่งว่า “eye of Quebec” เกิดขึ้นเมื่อประมาณ 212 ล้านปีที่แล้ว มีความกว้าง 3 กม.
8.Kara-Kul Lake, Tajikistan
หลุมอุกกาบาตที่อยู่สูงกว่าระดับน้ำทะเล 3,900 เมตร อยู่ใกล้ชายแดนประเทศจีน
7.Clearwater Lakes, Canada
เกิดจากอุกกาบาตที่พุ่งชนพร้อมกันสองลูก เมื่อประมาณ 290 ล้านปีที่ผ่านมา ปัจจุบันเป็นสถานที่ท่องเที่ยวยอดนิยม เนื่องจากความงดงามของท้องทะเลโดยรอบนั่นเอง
6.Mistastin Lake, Canada
ชนโลกเมื่อ 38 ล้านปีที่แล้ว กว้างประมาณ 28 กม.
5.Gosses Bluff, Australia
กระแทกโลกเมื่อ 142 ล้านปีก่อน แรงระเบิดของมันมีอาณุภาพทัดเทียมระเบิด TNT 22,000 เมกกะตัน
4.Aorounga Impact Crater, Chad
เกิดจากอุกกาบาตเส้นผ่านศูนย์กลาง 1.6 กม. ชนโลกเมื่อ 200-300 ล้านปีก่อน
3.Deep Bay, Canada
อยู่บริเวณ Saskatchewan, Canada การพุ่งชนก่อให้เกิดทะเลสาบลึก กินอาณาเขตถึง 13 กม.พุ่งชนเมื่อประมาณ 100 ล้านปีที่แล้ว
2.Lake Bosumtwi Crater, Ghana
หลุมนี้อยู่ห่างไป 30 กม.จากเมือง Kumasi, Ghana เป็นทะเลสาบธรรมชาติเพียงแห่งเดียวของที่นี่ เกิดจากการชนเมื่อประมาณ 1.3 ล้านปีที่แล้ว มีความลึก 10.5 กม. ล้อมรอบด้วยป่าดงดิบที่กินอาณาเขตกว้างขวาง
1.Barringer Crater, Arizona, US
ประมาณ 49,000 ปีที่แล้ว อุกกาบาตหนัก 1,000 ตัน โหม่งโลกด้วยความเร็วกว่า 40,000 ไมล์ต่อชั่วโมง ก่อให้เกิดหลุมลึก กินอาณาบริเวณถึง 55 กม.นับเป็นการชนที่รุนแรงที่สุดในประวัติศาสตร์โลก ความแรงของการระเบิดครั้งนั้นอานุภาพเทียบเท่ากับระเบิด TNT กว่า 20 ล้านตันเลยทีเดียว
ที่มาและภาพประกอบ : environmentalgraffiti.com
วันศุกร์ที่ 19 กันยายน พ.ศ. 2557
สัตว์ 12 ชนิดที่เราควรดีใจที่พวกมันได้สูญพันธุ์ไปแล้ว
เป็นความโชคดีของมนุษย์รุ่นเราๆ ที่ไม่ได้เกิดและใช้ชีวิตในยุคเดียวกับแมงป่องยักษ์และผองเพื่อน ลองไปดูกันว่าแต่ละตัวนั้นโหดร้ายและน่ากลัวยังไงกันบ้าง รับรองว่าเห็นแล้วคุณจะไม่หิวแน่นอน
1. จระเข้ยักษ์ (Purassaurus)
Via deviantart.com
Purassaurus เป็นจระเข้ยักษ์ที่อาศัยอยู่ในอเมริกาใต้เมื่อประมาณ 8 ล้านปีที่แล้ว วัดความยาวสูงสุดได้ถึง 13 เมตร ซึ่งยาวกว่า 2 เท่าของจระเข้สายพันธุ์ที่ยาวที่สุดที่ยังมีชีวิตอยู่ในปัจจุบัน
ทำไมต้องดีใจที่มันสูญพันธุ์ : ก็ตัวมันใหญ่กว่าจระเข้ในยุคนี้ตั้งสองเท่า ความน่ากลัวมันก็ต้องเพิ่มเป็นสองเท่าด้วยน่ะ
2. แมงป่องยักษ์ยาว 3 ฟุต (Pulmonoscorpius)
Via generalkulture.blogspot.co.uk
Pulmonoscorpius ก็มีลักษณะเหมือนแมงป่องในยุคปัจจุบันนี่หล่ะ ที่มีกรงเล็บอยู่ด้านหน้าและเหล็กในที่หางของมัน ต่างกันแค่ความยาวเท่านั้นเอง
ทำไมต้องดีใจที่มันสูญพันธุ์ : คุณคงไม่สามารถจับหางมันแล้วโยนออกไปนอกหน้าต่างเหมือนแมงป่องตัวเล็กๆที่คุณเคยเจอ กลับกันมันอาจจะเป็นฝ่ายที่เหวี่ยงคุณออกไปแทน!
3. กิ้งกือยักษ์ (Arthropleura)
Via geology.cz
Arthropleura ก็เหมือนกิ้งกือยุคนี้แหละครับ เพียงแต่มันมีความยาว 2 เมตร!
ทำไมต้องดีใจที่มันสูญพันธุ์ : อื้มม ช่างมันเหอะ...
4. แมงมุมที่มีเหล็กในเหมือนแมงป่อง (Attercopus)
Flo Perry / Via coo.fieldofscience.com
Attercopus เป็นแมงมุมรุ่นบุกเบิกที่รู้จักกันมาช้านาน นอกจากจะผลิตใยแมงมุมได้แล้ว ยังมีเหล็กในเหมือนแมงป่องด้วย
ทำไมต้องดีใจที่มันสูญพันธุ์ : คงไม่ดีแน่ถ้าแมงมุมและแมงป่องพันธุ์ที่ร้ายกาจที่สุด รวมตัวกันเป็นหนึ่งเดียว!
5. ปลาฉลามยักษ์ (Megalodon)
Flo Perry / Via bizarbin.com
Megalodon มีความยาวสูงสุดถึง 50 ฟุต
ทำไมต้องดีใจที่มันสูญพันธุ์ : ฟันของมันมีขนาดเฉลี่ยเท่ากับฝ่ามือคนเลยทีเดียวและมันก็ดุร้ายกว่าฉลามทั่วไปถึง 10 เท่า
6. สัตว์ประหลาดยักษ์ที่เป็นพันธุ์ผสมระหว่างกิ้งกือกับแมงป่องโดยอาศัยอยู่ในน้ำ (Jaekelopterus)
Via webecoist.momtastic.com
Jaekelopterus มีความยาว 2.5 เมตร และอาศัยอยู่ในน้ำ
ทำไมต้องดีใจที่มันสูญพันธุ์ : นักวิจัยบอกว่า ถ้ามีสัตว์ตัวอื่นอยู่ตรงหน้ามัน มันจะพุ่งเข้าหาและฉีกให้เป็นชิ้นเล็กชิ้นน้อย หลังจากนั้นก็ค่อยๆรับประทานทีละชิ้นๆ
7. ปลาปิรันย่ายักษ์ (Megapiranha)
Via cracked.com
Megapiranha มีชีวิตอยู่ในช่วง 8-10 ล้านปีที่แล้ว ความยาวประมาณ 1 เมตร
ทำไมต้องดีใจที่มันสูญพันธุ์ : เพราะว่า ปิรันย่าในปัจจุบัน = nightmares ปิรันย่ายักษ์ = never going anywhere near water ever again.
8. งูสายพันธุ์ที่ใหญ่ที่สุดในโลก (Titanoboa)
Via news.unl.edu
Titanoboa มีความยาวถึง 13 เมตร และหนักมากกว่า 1 ตัน อาศัยอยู่ในเขตร้อนช่วง 60 ล้านปีที่แล้ว
ทำไมต้องดีใจที่มันสูญพันธุ์ : เพราะมันจะกินเหยื่อโดยบดให้ละเอียดเหมือนงูเหลือมยักษ์ ละเอียดเหมือนยาสีฟันที่อยู่ในหลอดเลยหล่ะ
9. แมลงปอยักษ์ (Meganeura)
Via enaliaphysis.org.cy
Meganeura มีความยาวระหว่างปลายปีกทั้งสองข้างถึง 70 เซนติเมตร ประมาณแขนข้างหนึ่งของคนเราเลยทีเดียว
ทำไมต้องดีใจที่มันสูญพันธุ์ : เพราะคุณคงต้องใช้ไม้ตีแมลงขนาดใหญ่เท่าไม้พายเรือเพื่อที่จะไล่เวลามันมาเกาะที่ขนมปังทาแยมของคุณ
10. สัตว์ประหลาดใต้น้ำที่มีหน้าตาเหมือนกุ้งผสมกับปลาหมึก แถมมีฟันติดมาด้วย (Anomalcaris)
youtube.com / Via Flo perry
Anomalcaris มีเปลือกและหางเหมือนกุ้ง แต่มีหนวดและตาเหมือนปลาหมึก เพียงแต่มีฟันติดหนวดมาด้วย โตเต็มที่จะยาวประมาณ 60 เซนติเมตร อย่างไรก็ตามนักวิทยาศาสตร์บางคนเชื่อว่ามันน่าจะมีขนาดใหญ่กว่านั้น มีชีวิตอยู่ในช่วง 540ล้านปีที่แล้ว
ทำไมต้องดีใจที่มันสูญพันธุ์ : เพราะมันเป็นสัตว์กินเนื้อ ถ้ามันยังมีชีวิตอยู่ คุณอาจจะไม่มีโอกาสได้กินอาหารทะเลอร่อยๆอย่างทุกวันนี้ก็เป็นได้ เพราะจะโดนมันกินเรียบจนสูญพันธุ์กันหมด
11. ปลาหมึกกระดองยักษ์ (Cameroceras)
Via walkingpedia.wikia.com
จากซากกระดองที่ค้นพบคาดว่ามันน่าจะมีความยาวประมาณ 9 เมตร ถึงมันจะเป็นสัตว์ที่ตาแทบจะมองไม่เห็น แต่มันก็เป็นนักล่าที่ค่อนข้างน่ากลัวเลยทีเดียว มันน่าจะเป็นสัตว์ที่มีขนาดใหญ่ที่สุดในมหาสมุทรในช่วงที่มันยังมีชีวิตอยู่ 470 ล้านปีที่แล้ว
ทำไมต้องดีใจที่มันสูญพันธุ์ : เพราะหนวดมันใหญ่มาก และคงไม่ได้ใช้ประโยชน์อะไรจากหนวดมันในโลกปัจจุบันนี้ ก็เท่านั้นเอง
12. เพนกวินที่มีขนาดเท่ามนุษย์ (Palaeeudyptes klekowskii)
Via ecolounge.hu
Palaeeudyptes klekowskii มีชีวิตอยู่ในช่วง 37 ล้านปีที่แล้ว เวลายืนจะสูงประมาณ 2 เมตร
ทำไมต้องดีใจที่มันสูญพันธุ์ : คุณอาจจะคิดว่าน่าจะดี ถ้ามันยังมีชีวิตอยู่ แต่คงไม่เข้าท่า ถ้าคุณพยายามจะกอดมัน แต่อาจจะโดนเฉาะหัวด้วยจงอยปากอันใหญ่ยักษ์ของมัน
http://board.postjung.com/805492.html#
วันอังคารที่ 16 กันยายน พ.ศ. 2557
"8 สิ่ง" ที่รถไฟญี่ปุ่นไม่เหมือนรถไฟไทย
วันนี้จะพาไปเจอกับคอลัมน์ JaPON JaPAN(เจปง เจแปน) สำหรับวันนี้ได้นำเรื่องเกี่ยวกับรถไฟญี่ปุ่นมาฝาก มาดูกันให้เห็นชัดๆ ว่ารถไฟของประเทศที่ขึ้นชื่อเรื่องความเป๊ะ ความเนี้ยบ และความตรงเวลาอย่างญี่ปุ่นมีอะไรที่น่าสนใจที่รถไฟประเทศเราไม่มี เชื่อว่าหลายๆ อย่างนับว่าดีมากหากมาประยุกต์ใช้กับรถไฟบ้านเรา เลยเอามาแชร์ให้อ่านกันค่ะ^^
1. โบกี้สำหรับผู้หญิง (女性専用)
ที่ญี่ปุ่น ในรถไฟหนึ่งขบวนจะมีสักหนึ่งโบกี้ที่จัดไว้ให้สำหรับผู้หญิงโดยเฉพาะ ยิ่งช่วงเวลาเร่งด่วน รถไฟญี่ปุ่นเบียดสุดๆ เบียดแบบชนิดที่ว่าพี่โชไม่ไหวแล้ว เอาเป็นว่าถึงขั้นแก้มแนบแก้ม ก้นแนบก้น อกแนบอก (พูดจริงๆ ไม่ได้ทะลึ่ง) รับรู้ได้ถึงชีพจรของแต่ละคนที่ยืนติดกับเราเป็นเสียง ตุ้บ ตุ้บ เลยทีเดียว ยิ่งต้องหายใจร่วมกัน (คือยิ่งกว่าหายใจรดต้นคออีกอะ) แทบพลีชีวิต พูดตรงๆ เลยว่าบางทีรอบตัวมีแต่คุณลุงหน้าตาหื่นๆ อาบน้ำตอนเช้ารึเปล่าไม่รู้ ขนาดพี่โชเป็นผู้ชายยังสยอง ก็ไม่แปลกที่สาวๆ ญี่ปุ่นหลายคนไม่กล้าจะขึ้นไปเบียดด้วยสภาพนั้น
ทางการญี่ปุ่นจึงจัดให้รถไฟซักโบกี้นึงเป็นโบกี้เฉพาะสำหรับผู้หญิง โดยเฉพาะเวลาเร่งด่วนที่เบียดๆ สาวๆ ทั้งหลายจะได้ไม่ต้องกลัวโดนลวนลามหรือเบียดกับผู้ชายในตู้ทั่วไป โดยมากตู้สำหรับผู้หญิงจะเป็นช่วงเวลาเช้าและเลิกงานที่คนเยอะจริงๆ ในระหว่างวันตู้นั้นผู้ชายก็สามารถขึ้นได้ตามปกติครับ ใครจะไปญี่ปุ่นโดยเฉพาะโตเกียวลองสังเกตสติกเกอร์สีชมพูๆ แบบนี้ให้ดีนะครับ เป็นประโยชน์แน่นอนเพราะหมายถึงตู้นั้น สำหรับผู้หญิงขึ้นโดยเฉพาะ ตู้แบบนี้มีไว้ก็ไม่เลวเลยใช่มั้ยล่ะ สาวๆ คนไหนใคร่ขึ้น...ขึ้น ใครใคร่ขึ้นขบวนเบียดกับผู้ชาย...เบียด 555
2. โบกี้สำหรับคนขี้หนาว(弱冷房車)
ด้วยความขี้หนาวของคนญี่ปุ่นนี้เอง ก็ไม่แปลกที่ญี่ปุ่นจะมีรถไฟบางขบวนที่เปิดแอร์เบาๆ เบาแบบว่าบางทีพ่นลมเฉยๆ ไม่ปรับอุณหภูมิ จริงๆ นะ ไม่ได้หลอก เรียกกันว่าเปิดแบบ 送風 ใครอ่านตัวจีนออกก็จะเข้าใจทันทีว่าแปลว่า พ่นลม/ส่งลม การเปิดแอร์แบบนี้ คนไทยที่เพิ่งมาญี่ปุ่น พี่โชมั่นใจว่าตายยยยยยแน่ๆ
รถไฟหลายๆ ขบวนที่ญี่ปุ่นมักจะมีรถไฟสำหรับคนขี้หนาวนี้อยู่ นั่นหมายถึง หน้าร้อนจะเปิดแอร์ไม่แรง แต่หน้าหนาวโบกี้นี้ก็จะอุ่นกว่าโบกี้อื่นๆ ถ้าใครมาญี่ปุ่นก็อย่าลืมสังเกตสัญลักษณ์แอร์เบานี้ด้วยนะครับ ไม่งั้นต้องทนร้อนไปตลอดทาง ไอเดียนี้ที่ไทยน่าจะเอาไปประยุกต์เป็นขบวนแอร์แรง พี่โชว่าคนขึ้นกันตรึม
3. แยกแถวต่อสำหรับคนที่จะขึ้นก่อนขึ้นหลัง (先発列車・次発列車)
อันนี้อาจงงหน่อย แต่เหมาะมากในการสร้างระเบียบในการต่อแถวครับ ยกตัวอย่างเช่น เรากำลังจะกลับบ้านด้วยรถด่วน แต่รถที่มาถึงก่อนเป็นรถแบบจอดทุกสถานี (หวานเย็น) ที่ญี่ปุ่นก็จะมีที่ยืนให้เราต่อแถวรอรถขบวนต่อไปแบบไม่เกะกะคนที่จะขึ้นรถขบวนก่อนเรา โดยเขียนเป็นเส้นที่พื้น ปัดหางแถวสวยงามไม่ขวางทางใคร ป้องกันการแซงแถวและการยืนออกันมั่วๆ ซึ่งอาจสร้างความลำบากแก่คนขึ้นลงขบวนก่อนหน้าเรา
ด้วยเหตุนี้ ญี่ปุ่นจึงดูเป็นประเทศที่เป็นระเบียบมากเวลาจะขึ้นหรือลงรถไฟ นอกจากจะสวยงามน่าดูชมแล้ว ยังไม่ก่อให้เกิดความเครียดจากการแย่งชิงเพราะไม่ต่อแถวอีกด้วย
4. ไม่ใช้มือถือพูดคุยเด็ดขาด(車内通話禁止)
อันนี้อาจจะโหดไปหน่อยสำหรับสังคมไทย แต่ที่ญี่ปุ่นเป็นเรื่องปกติมากที่จะไม่พูดโทรศัพท์ในที่สาธารณะ โดยเฉพาะในรถไฟนี่แทบจะเรียกว่าต้องห้ามเลยด้วยซ้ำ ใครหยิบโทรศัพท์ขึ้นมา “ฮัลโหลลลลล” เมื่อไหร่นี่โดนมองตั้งแต่หัวจรดเท้าแน่นอน
ตอนที่พี่โชมาญี่ปุ่นใหม่ๆ ก็สุดแสนจะอึดอัดที่ไม่สามารถจะคุยโทรศัพท์ด้วยเสียงในรถไฟได้ แต่อยู่ไปนานๆ ก็เริ่มชิน แถมสมัยนี้มี application ให้เล่นได้มากมาย ไม่คุยโทรศัพท์ในรถไฟจึงเป็นเรื่องไม่ยากแล้วเพราะมีอะไรให้ทำแทน
บางคนอาจถามว่าทำว่าทำไมที่ญี่ปุ่นต้องซีเรียสกับการห้ามคุยโทรศัพท์บนรถไฟด้วย เหตุผลแรกๆ เลยคือ มารยาทครับ มีงานสำรวจความเห็นคนญี่ปุ่น สิ่งที่น่ารำคาญที่สุดบนรถไฟคือเสียงโทรศัพท์เรียกเข้าและเสียงการคุยโทรศัพท์ ถ้าใครนึกไม่ออกว่าน่ารำคาญยังไง ให้นึกถึงเสียงริงโทนแสนแซ่บเมกะฮิตซ์แดนซ์กระจายในรถไฟบ้านเรา หรือคนที่นั่งเม้าท์โทรศัพท์ตลอดทาง จนเราซึ่งแอบฟังอยู่แทบจะช่วยนางออกความเห็นตามไปด้วย ฮ่าๆ
5. ต้องปิดสัญญาณมือถือในที่นั่งคนชรา หญิงมีครรภ์ ผู้มีปัญหาทางร่างกาย(優先席携帯電話OFF)
นอกจากจะไม่ค่อยเจอคนคุยด้วยเสียงดังในรถไฟแล้ว ที่ญี่ปุ่นจะมีการแบ่งที่นั่งที่หัวหรือท้ายขบวนให้กับผู้ชรา หญิงมีครรภ์ และคนที่อาจมีปัญหาทางร่างกาย เป็นต้น ที่นั่งนี้จะมีป้ายเขียนประมาณว่า...นอกจากเราจะต้องสละที่นั่งให้พวกเขาเหล่านั้นก่อนแล้ว หากอยากอยู่บริเวณนั้น ก็ต้องปิดสัญญาณสื่อสารให้หมดด้วย พูดง่ายๆ คือปิดมือถือนั่นเอง
ตอนแรกๆ พี่ก็สงสัยว่าทำไมต้องปิดเครื่อง แค่ปิดเสียงไม่พอหรือไง อะไรเนี่ย งงมาก แต่พอได้รู้เหตุผลก็ถึงกับทึ่งและซึ้งใจ ที่ต้องปิดเครื่องนั้นเป็นเพราะบางคนอาจใช้เครื่องช่วยฟัง เครื่องนับก้าว เครื่องที่เกี่ยวกับผู้ป่วยโรคหัวใจ หรือเครื่องมือทางการแพทย์ใดๆ ที่ผู้ป่วยใส่อยู่ หากมีสัญญาณมือถือรบกวนอาจทำให้เครื่องนั้นทำงานได้ไม่เต็มที่
ลองนึกง่ายๆ ดู ใครเคยเอามือถือไปวางใกล้ลำโพงแล้วพอมีสายเรียกเข้า จะมีเสียงตือดือดึดๆๆ แปลกประหลาดบ้าง นั่นแหละ น่าจะคล้ายกัน ซึ่งผู้ที่ใช้เครื่องมือทางการแพทย์อาจโดนสัญญาณรบกวนแบบนั้นจริงๆ นับถือคนญี่ปุ่นจริงๆ ที่คิดคำนึงถึงคนอื่นแม้แต่เรื่องเล็กๆ ที่ตามองไม่เห็นแบบนี้
6. การขึ้นบันไดเลื่อน(エスカレーターの立ち位置)
ประเด็นนี้ยังเป็นที่ถกเถียงกันอยู่ไม่ว่าจะที่ไทยหรือที่ไหนๆ ว่า เวลาขึ้นบันไดเลื่อนต้องชิดซ้ายหรือชิดขวากันแน่?? อย่างที่โตเกียว คนส่วนมากจะชิดซ้าย ส่วนที่โอซาก้า คนจะชิดขวากันหมด เช่นเดียวกับที่เรากำลังรณรงค์กันในรถไฟฟ้าและรถไฟใต้ดินที่กรุงเทพฯ
จริงๆ ที่ญี่ปุ่นมีการชิดด้านใดด้านหนึ่งอย่างเป็นระเบียบนี้มานานมากแล้ว ในขณะที่บ้านเรากำลังเริ่มต้นรณรงค์จริงจัง แต่ที่น่าแปลกใจคือ ตอนนี้ที่ญี่ปุ่นกำลังกลับไปสู่จุดเริ่มต้น พยายามให้คนยืนทั้งสองฝั่งของบันไดเลื่อน ด้วยเหตุผลด้านความปลอดภัยบ้างล่ะ จะได้ไม่มีคนวิ่งบนบันไดเลื่อน หรือด้วยเหตุผลของการบำรุงรักษา เพราะถ้ายืนออกันด้านเดียวอาจเกิดความไม่สมดุลของบันไดเลื่อน ก็ว่ากันไป (เท่าที่ได้ยินมาเป็นแบบนี้)
ด้วยเหตุนี้ หลายๆ ที่ในญี่ปุ่นในตอนนี้ แทนที่จะให้ยืนชิดด้านใดด้านหนึ่ง เราจะเห็นป้ายที่เขียนว่าให้ยืนทั้งสองฝั่งแทน เอ๊ะ อะไรยังไง? ที่ไทยรณรงค์แทบตายให้ยืนชิดขวาเป็นระเบียบ ทำไมญี่ปุ่นกลับตรงกันข้ามกันล่ะเนี่ย ต้องติดตามกันต่อไปครับ
7. พนักงานช่วยยัดคนลงไปในรถไฟ (満員電車に乗客を押し込む駅員)
ตอนชั่วโมงเร่งด่วน รถไฟในโตเกียวโดยเฉพาะสายจากชานเมืองเข้ามาตัวเมือง อัดแน่นยิ่งกว่าอะไรในโลกใบนี้สิ่งที่ขาดไม่ได้เลยคือนายสถานีที่ต้องทำหน้าที่พิเศษ นั่นคือคอยผลักและยัดผู้โดยสารเข้าไปในรถให้ได้มากที่สุด
8. ใบแจ้งว่ามาสายเพราะรถไฟ(遅延証明書)
สมมติว่าวันไหนเกิดเหตุที่ทำให้รถไฟมาช้า แล้วทำให้เราไปโรงเรียนหรือที่ทำงานไม่ทัน ที่สถานีรถไฟจะมีกระดาษวางตั้งเอาไว้ให้เราหยิบไปเป็นหลักฐานว่าไม่ใช่ความผิดของเรานะ แต่เป็นเพราะรถไฟช้า หัวหน้าหรืออาจารย์จะได้ไม่สามารถเอาผิดเราได้ บางที่มีให้เลือกหยิบได้ว่าสายไปแล้วกี่นาทีแบบในรูปที่พี่โชหามาให้ดู เขาเขียนเป็นเลขเวลา 10 20 30 นาทีเลยทีเดียว แหม อยากให้ที่จ่ายเงินทางด่วนบ้านเรามีใบนี้ให้หยิบบ้างจังเลย
Cradit:http://board.postjung.com/804665.html,Dek-D.com
วันจันทร์ที่ 15 กันยายน พ.ศ. 2557
คำถามคณิต 7 ข้อ ที่ยากที่สุดในโลก
ปี 1900 ในงานประชุมสัมมนาของเหล่านักคณิตศาสตร์ ฮิลเบอร์ต ได้นำเสนอปัญหายี่สิบสามข้อ ซึ่งเป็นปัญหาที่น่าสนใจและยังไม่มีใครทราบคำตอบในสมัยนั้น
หนึ่งร้อยปีผ่านไป ปัญหาเหล่านั้นหลายข้อได้รับคำตอบและมีบทพิสูจน์ยืนยันเป็นที่น่าพอใจ ปัญหาบางส่วนยังไม่มีใครตอบได้ และในขณะเดียวกัน เมื่อโลกหมุนไปก็มีวิทยาการใหม่ๆ มีคำถามใหม่ๆที่รอคำตอบมากขึ้น
รีมันน์พบว่าสมการนี้มีคำตอบมากมายเหลือเกิน ตั้งแต่จำนวนเต็มลบคู่ทั้งหมด (ได้แก่ -2,-4,-6,...) และอีก "ส่วนหนึ่ง" ที่รีมันน์ไม่สามารถหาค่าได้หมด และไม่ทราบว่ามีอะไรบ้าง
คำถามล้านที่สามนี้ถามว่า จริงหรือไม่ที่คำตอบอีก "ส่วนหนึ่ง" ที่เหลือนั้นจะต้องเป็นจำนวนเชิงซ้อนที่มีส่วนจริง (real part) เท่ากับ 1/2
Birch and Swinnerton-Dyer Conjecture เป็นปัญหาคณิตศาสตร์บริสุทธิ์เกี่ยวกับสมการหลายตัวแปรที่ต้องการคำตอบเป็นจำนวนเต็ม สมการที่ดูเหมือนง่ายๆนั้น ในบางกรณีก็ไม่มีคำตอบที่เป็นจำนวนเต็ม อย่างเช่น ไม่มีจำนวนเต็ม x และ y ใดๆ ที่ทำให้ หรือที่โด่งดังกว่านั้นก็คือสมการ สำหรับ n มากกว่า 2 ที่รู้จักกันในนาม Fermat's last theorem หรือ ทฤษฎีบทสุดท้ายของเฟอร์มาต์
ก่อนที่เฟอร์มาต์จะเสียชีวิต เขาได้ทิ้งมรดกชิ้นสำคัญไว้ให้กับนักคณิตศาสตร์รุ่นหลังชิ้นหนึ่ง นั่นคือสมุดบันทึกสูตรและบทพิสูจน์ต่างๆที่เขาค้นพบในช่วงยังมีชีวิต Fermat's last theorem เป็นทฤษฎีบทสุดท้ายในสมุดบันทึกเล่มนั้น น่าเสียดาย เฟอร์มาต์ไม่ได้ทิ้งบทพิสูจน์ไว้ บอกเพียงแต่ว่าหน้ากระดาษไม่พอเขียนเท่านั้น แต่ผลปรากฏก็คือว่า ในยุคนั้นไม่มีใครเติมเต็มชิ้นส่วนที่หายไปนี้ได้ ทฤษฎีบทสุดท้ายของเฟอร์มาต์เป็นปัญหาคาใจของเหล่านักคณิตศาสตร์อยู่หลายชั่วอายุคน
เวลาผ่านไปร่วมสามร้อยปี จนในปี 1994 Andrew Wiles ก็สามารถพิสูจน์ทฤษฎีบทสุดท้ายของเฟอร์มาต์ได้ โดยพิจารณาสมการ ด้วยความเป็นกราฟ และเรียกชื่อกราฟนั้นว่า elliptic curve และก็ด้วยเหตุนี้เอง elliptic curve จึงเป็นที่สนใจของบรรดาเหล่านักคณิตศาสตร์ และเป็นกุญแจสำคัญของ Birch and Swinnerton-Dyer Conjectur
หนึ่งร้อยปีผ่านไป ปัญหาเหล่านั้นหลายข้อได้รับคำตอบและมีบทพิสูจน์ยืนยันเป็นที่น่าพอใจ ปัญหาบางส่วนยังไม่มีใครตอบได้ และในขณะเดียวกัน เมื่อโลกหมุนไปก็มีวิทยาการใหม่ๆ มีคำถามใหม่ๆที่รอคำตอบมากขึ้น
ประวัติศาสตร์จึงต้องกลับมาย้อนรอย ในขณะที่โลกเฉลิมฉลองศตวรรษใหม่ในปี 2000 สถาบันคณิตศาสตร์เคลย์ (Clay Mathematics Institute) ก็ได้ร่วมเฉลิมฉลองโดยการคัดเลือกเจ็ดโจทย์ปัญหาคณิตศาสตร์ที่ได้ชื่อว่า "ยาก" ที่สุด และ "สำคัญ" ที่สุดในช่วงศตวรรษนี้ ในโจทย์เจ็ดข้อนี้มีหลายข้อที่เป็นคณิตศาสตร์ล้วน แต่ก็มีหลายข้อที่เป็นคำถามจากนักเขียนโปรแกรม เป็นข้อสงสัยจากวิศวะ เป็นสมการจากฟิสิกส์ ในงานประชุมของเหล่านักคณิตศาสตร์ในปีนั้น สถาบันคณิตศาสตร์เคลย์ได้ขนานนามโจทย์เจ็ดข้อนั้นว่า Millennium Problems และนำเสนอเงินรางวัลหนึ่งล้านเหรียญสหรัฐให้กับผู้ที่สามารถพิชิตโจทย์แต่ละข้อเหล่านี้ได้ เงินรางวัลจำนวนมหาศาลนี้ไม่ได้เป็นเพียงเครื่องเรียกร้องความสนใจจากนักข่าวและนักคณิตศาสตร์ทั่วทุกมุมโลกเท่านั้น แต่เป็นหลักฐานที่บ่งบอกถึงความยากและความเจริญก้าวหน้าที่คำตอบของโจทย์เหล่านี้จะนำมาสู่โลกด้วย
ผู้เขียนเองมีความรู้ความสามารถน้อย ทั้งในด้านวิชาการและในด้านการถ่ายทอด ในบางกรณีจึงไม่สามารถเข้าใจคำถามของโจทย์ได้อย่างแจ่มแจ้ง และในบางกรณีก็ไม่สามารถอธิบายคำถามของโจทย์ได้ครอบคลุมทั้งหมด ต้องอาศัยการอุปมาแทนการใช้คำศัพท์เฉพาะทางที่ตรงไปตรงมา จึงต้องขออภัยมา ณ ที่นี้ด้วย อนึ่ง โจทย์ปัญหาเหล่านี้ล้วนเป็นโจทย์ชื่อดัง ท่านผู้อ่านที่สนใจสามารถหาอ่านรายละเอียดเชิงลึกเพิ่มเติมได้ไม่ยากบนอินเตอร์เนต
P vs NP
ปัญหา P vs NP แทบจะกล่าวได้ว่าเป็นปัญหาที่สำคัญที่สุดในวงการนักเขียนโปรแกรม เพราะโปรแกรมถึงจะดีขนาดไหน แต่ถ้าทำงานช้ายืดยาดเหลือเกิน ก็คงไม่มีใครอยากใช้
นักคอมพิวเตอร์จึงต้องจัดประเภทของรูปแบบของงานตามความเร็วที่คอมพิวเตอร์จะสามารถทำได้
"P" (Polynomial time) คือรูปแบบของงานที่คอมพิวเตอร์สามารถทำได้เร็ว
"E" (Exponential time) คือรูปแบบของงานที่ต้องใช้เวลามาก อาจต้องใช้เวลาเป็นล้านๆปี
แต่รูปแบบงานทั่วไปของโรงงานอุตสาหกรรมห้างร้านทั้งหลาย ยากกว่าแบบ P แต่ก็ไม่ได้ยากเหมือนแบบ E จึงอยู่ตรงกลางและได้ชื่อว่ามีรูปแบบ "NP" (Nondeterministic Polynomial time) แต่ก็มีความเชื่อที่ว่างานในรูปแบบ NP นั้น ในความเป็นจริงอาจจะง่ายเหมือนอย่างงานในรูปแบบ P ก็ได้ เพียงแต่ยังไม่มีใครรู้วิธีเท่านั้นเอง
ถ้าจะมีเครื่องคิดเลขสักเครื่องแล้วคนคนหนึ่งอยากรู้ว่า 3329 คูณ 4547 ได้เท่าไหร่ กดเครื่องคิดเลขแปบเดียวก็ตอบได้แล้วว่าผลลัพท์คือ 15136963 แต่ในขณะเดียวกัน ถ้าจะมีคนอีกคนหนื่งอยากรู้ว่า 15136963 เท่ากับเลขใดคูณกัน เขาอาจต้องใช้เวลาเป็นวันๆในการกดเครื่องคิดเลขไล่ไปเรื่อยๆ การ "คูณ" นั้น สำหรับคอมพิวเตอร์แล้วเป็นงานที่ง่าย เป็นงานในรูปแบบ P แต่การ "แยกตัวประกอบ" นั้นเป็นงานที่ยาก เป็นงานในรูปแบบ NP แต่ทั้งนี้ ไม่มีใครแน่ใจว่า "งานที่ยาก" นั้น ยากโดยตัวของมันเอง หรือยากเพราะมนุษย์เรายังไม่รู้วิธีจัดการที่เหมาะสม
คำถามหนึ่งล้านแรกนี้ก็คือ จริงหรือไม่ที่ งานในรูปแบบ NP ง่ายเหมือนงานในรูปแบบ P
ภาพ: ตัวอย่างงานในรูปแบบ P และ NP
ปัญหา P vs NP จึงเป็นเหมือนคำถามซ้อนคำถาม เพราะ P และ NP เองที่จริงก็คือรูปแบบของคำถามนี่เอง นักวิจัยส่วนที่เชื่อว่า P=NP จะพยายามหาวิธีแก้ปัญหาในรูปแบบ NP ให้เร็วขึ้น หากทำได้จริง คอมพิวเตอร์จะสามารถทำงานได้เร็วขึ้น ระบบอินเตอร์เนตและเครือข่ายสัญญาณทุกรูปแบบจะมีวิธีปรับปรุงใหม่ โรงงานอุตสาหกรรมจะถูกออกแบบให้มีประสิทธิภาพมากขึ้น เส้นทางเดินเรือและระบบส่งสินค้าจะได้รับการพัฒนา
เสน่ห์อย่างหนึ่งของโจทย์ปัญหาข้อนี้ก็คือ หาก P=NP จริง การพิสูจน์ว่า P=NP จะสามารถทำได้โดยใช้ความคิดสร้างสรรค์ล้วนๆไม่ต้องใช้คณิตศาสตร์เลย หากจะมีเด็กประถมสมองใส หาวิธีการทำงานหนึ่งงานใดในรูปแบบ NP-complete ให้เสร็จอย่างรวดเร็วได้ ก็จะได้ชื่อว่าพิชิตปัญหา P vs NP แล้ว จะอย่างไรก็ดี แม้แต่ผู้เชี่ยวชาญที่ทุ่มเทเวลาให้กับงานวิจัยก็ยังไม่พบวิธีแก้ปัญหาเหล่านั้น
ภาพ: มุขตลกบนแผ่นรองเมาส์ว่าปัญหา P vs NP แก้ได้ด้วยการทานกาแฟน้อยๆ
Poincare Conjecture
ในปี 1904 พอย์นคาเร่ ได้ตีพิมพ์ผลงานวิจัยเกี่ยวกับ คุณสมบัติของรูปทรง และมิติสัมพันธ์ขึ้นมาฉบับหนึ่ง ในตอนท้ายของรายงายฉบับนั้น มีข้อติดข้องประการหนึ่งที่พอย์นคาเร่หาคำตอบไม่ได้ จนพอย์นคาเร่เสียชีวิตและนักคณิตศาสตร์หลายต่อหลายคนพยายามหาคำตอบให้กับปัญหานั้น แต่ไม่มีใครทำสำเร็จ ปัญหานั้นจึงได้รับการขนานนามว่า Poincare Conjecture แปลห้วนๆก็คือ ข้อคาดเดาของพอย์นคาเร่ นั่นเอง
Poincare Conjecture เป็นคำถามเกี่ยวกับรูปทรงในสี่มิติ หากจะลองจินตนาการถึงผลส้ม ถ้าเอายางหนังสติ๊กไปรัดผลส้มไว้ ก็แน่นอนว่าหนังสติ๊กจะกระเด็นออกมาได้โดยที่ผลส้มยังคงทรงรูปร่างเดิม แต่หากจะจินตนาการใหม่ถึงโดนัท ถ้าเอายางหนังสติ๊กไปร้อยผ่านรูของโดนัทไว้ ก็เป็นไปไม่ได้ที่หนังสติ๊กจะกระเด็นออกมาโดยที่โดนัทยังทรงรูปร่างเดิม จึงกล่าวได้ว่าผลส้มและโดนัทมีความแตกต่างกันในเชิงมิติสัมพันธ์
คำถามล้านที่สองก็คือ รูปทรงในมิติที่สี่ที่มีคุณสมบัติแบบผลส้มมีอะไรบ้าง
ในสายตาของนักฟิสิกส์แล้ว มิติที่สี่ไม่ได้เป็นแค่จินตนาการไร้สาระ ลูกโลกมีลักษณะเป็นทรงกลมสามมิติ แต่เพราะเราซึ่งมีขนาดเล็กกว่าโลกมากและอาศัยอยู่บนพื้นผิวของโลก ในสมัยก่อนคนเราจึงเชื่อว่าโลกแบน จนต่อมานักดาราศาสตร์จึงได้คำนวนพิสูจน์ว่าโลกกลม ในทำนองเดียวกัน ก็มีความเป็นไปได้ว่าอันที่จริงจักรวาลอาจจะมีสี่มิติ แต่เพราะเราอาศัยอยู่บนพื้นผิวของจักรวาล จักรวาลจึงปรากฏกับเราว่ามีแค่สามมิติ
ภาพ: ปกวารสาร Science ให้เกียรติบทพิสูจน์ของ Poincare Conjecture
จะอย่างไรก็ดีนะคะ เป็นที่ยอมรับกันว่า Grigori Perelman พิสูจน์ Poincare Conjecture ได้เรียบร้อยแล้ว ณ เวลานี้ Poincare Conjecture เป็นปัญหาข้อเดียวในเจ็ดข้อที่มีบทพิสูจน์เป็นที่ยอมรับ
Riemann Hypothesis
Riemann Hypothesis หรือสมมุติฐานของรีมันน์ อาจจะเป็นปัญหาที่อายุยืนที่สุดในเจ็ดข้อ และเป็นหนึ่งในปัญหาของฮิลเบอร์ตในปี 1900 ที่หลงเหลือมาจนทุกวันนี้ ถ้าจะว่าให้เข้าใจง่ายที่สุด Riemann Hypothesis ก็เป็นโจทย์แก้สมการดีๆนี่เอง
รีมันน์ได้ศึกษาฟังก์ชันตัวหนึ่งซึ่งมีชื่อว่า zeta function และมีนิยามบนจำนวนที่มากกว่า 1 ว่า
zeta function นี้สามารถขยายนิยามออกไปได้แม้สำหรับค่า s ที่เป็นจำนวนเชิงซ้อน สิ่งที่รีมันน์สนใจในอันดับต่อไปก็คือ การหาค่า s ในสมการ
คำถามล้านที่สามนี้ถามว่า จริงหรือไม่ที่คำตอบอีก "ส่วนหนึ่ง" ที่เหลือนั้นจะต้องเป็นจำนวนเชิงซ้อนที่มีส่วนจริง (real part) เท่ากับ 1/2
ภาพ: ค่าของ zeta function ที่ได้จากโปรแกรม Mathematica
จะอย่างไรก็ดีนะ การแก้สมการดังกล่าวนี้ไม่ตรงไปตรงมาอย่างที่คิด เพราะเมื่อฟังก์ชันถูกขยายนิยามไปบนจำนวนเชิงซ้อนแล้วเรื่องประหลาดอาจเกิดขึ้นได้มากมายไม่รู้จบ อย่างเช่น ฟังก์ชันเอกซ์โปเนนเชียลธรรมดาๆอย่าง e^x นั้น พอไปอยู่บนแกนจำนวนเชิงซ้อนแล้วจะกลับกลายเป็นฟังก์ชันตรีโกณมิติไป แต่ zeta function นี้ซ้ำร้ายยิ่งไปกว่านั้น บนจำนวนเชิงซ้อน zeta function จะไม่มีนิยามที่ตรงไปตรงมา แต่ต้องอาศัยฟังก์ชันอื่นๆอีก
zeta function มีความสัมพันธ์โดยตรงกับจำนวนเฉพาะ (จำนวนที่แยกตัวประกอบไม่ได้ เช่น 2,3,5,7,11,13,17,19,23,29,...) ไม่มีใครรู้สูตรสำเร็จในการหาค่าจำนวนเฉพาะ แต่บทพิสูจน์ของ Riemann Hypothesis จะมีประโยชน์ในการศึกษาการกระจายตัวของจำนวนเฉพาะ หากจะถามว่าทำไมต้องศึกษาการกระจายตัวของจำนวนเฉพาะ? คำตอบก็คือเพราะจำนวนเฉพาะเป็นกระดูกสันหลังของระบบรหัสที่ใช้ในการสื่อสารทุกวันนี้ หากไม่มีการศึกษาเรื่องจำนวนเฉพาะมาก่อน อินเตอร์เนตจะไม่มีความปลอดภัยเลย อีเมลจะถูกแฮคได้ทุกเมื่อ ความลับของบริษัทจะถูกโจมตีเมื่อไหร่ก็ได้
จนถึงทุกวันนี้ นักคณิตศาสตร์ได้ใช้ซุปเปอร์คอมพิวเตอร์หาคำตอบของสมการเป็นล้านๆค่าแล้ว แต่ก็ไม่พบค่าใดที่ขัดแย้งกับ Riemann Hypothesis
Navier-Stokes Equations
ท่ามกลางปรากฏการณ์ธรรมดาๆอย่างเช่น กระแสน้ำในทะเล คลื่นจากท้ายเรือข้ามฟาก ควันธูปที่ลอยไปในอากาศ ทิศทางของก้อนเมฆ ก็ยังมีสิ่งที่นักวิทยาศาสตร์ไม่รู้ไม่เข้าใจแฝงอยู่เต็มไปหมด นักฟิสิกส์เชื่อว่า ท่ามกลางความยุ่งเหยิงและการเคลื่อนที่อย่างไม่เป็นระบบระเบียบของของเหลวและก๊าซทั้งหลายนั้น จะต้องมี "กฏ" บางอย่างที่สามารถอธิบายและพยากรณ์การเคลื่อนที่ที่ดูประหนึ่งว่าไม่มีทิศทางนั้นได้ คำตอบของ Navier-Stokes Equations จะเป็นที่มาของกฏนั้น
คนที่เรียนวิศวะและฟิสิกส์ในมหาวิทยาลัย อาจจะเคยเรียนวิชา fluid mechanics และปวดหัวกับการแก้ differential equation เพื่อหาอัตราการกระจายตัวของของเหลวหรือก๊าซมาแล้ว ในทำนองเดียวกัน Navier-Stokes Equations เป็นสมการดิฟฟีเรนเชียลที่อธิบายการเคลื่อนที่ของของไหล แต่มีเงื่อนไขมากมายและเขียนใหม่ได้หลายรูปแบบ จะอย่างไรก็ดี หนึ่งในสมการหลักๆก็คือ
คำถามล้านที่สี่ก็คือ Navier-Stokes Equations มีคำตอบหรือไม่
จนถึงทุกวันนี้ แม้แต่ในเงื่อนไขที่ง่ายที่สุด ก็ยังไม่มีใครสามารถหาคำตอบของสมการดังกล่าวได้ ไม่มีใครสามารถบอกได้ว่าคำตอบมีหรือไม่มี และไม่มีใครสามารถบอกได้ว่าถ้ามีคำตอบ คำตอบนั้นจะมีคุณสมบัติอะไรบ้าง ในความเป็นจริงแล้ว คำตอบของ Navier-Stokes Equations มีความจำเป็นในการสร้างรถเรือและเครื่องบินที่มีความเร็วสูง นักวิศวกรจึงต้องอาศัยคอมพิวเตอร์หาคำตอบตามสถานการณ์เป็นครั้งๆไป
Navier-Stokes Equations เป็นประหนึ่งน้องๆของทฤษฏีแห่งความยุ่งเหยิง คำตอบของสมการนี้จะเป็นประโยชน์อย่างมหาศาล กระแสน้ำและคลื่นลมจะได้รับการอธิบาย การพยากรณ์อากาศจะแม่นยำมาก ระบบเตือนซึนามิและพายุจะมีประสิทธิภาพเพิ่มขึ้น จะมีรถและเครื่องบินยุคใหม่ แม้แต่ในวงการแพทย์ก็จะเข้าใจระบบไหลเวียนโลหิตดีขึ้น
Birch and Swinnerton-Dyer Conjecture
ก่อนที่เฟอร์มาต์จะเสียชีวิต เขาได้ทิ้งมรดกชิ้นสำคัญไว้ให้กับนักคณิตศาสตร์รุ่นหลังชิ้นหนึ่ง นั่นคือสมุดบันทึกสูตรและบทพิสูจน์ต่างๆที่เขาค้นพบในช่วงยังมีชีวิต Fermat's last theorem เป็นทฤษฎีบทสุดท้ายในสมุดบันทึกเล่มนั้น น่าเสียดาย เฟอร์มาต์ไม่ได้ทิ้งบทพิสูจน์ไว้ บอกเพียงแต่ว่าหน้ากระดาษไม่พอเขียนเท่านั้น แต่ผลปรากฏก็คือว่า ในยุคนั้นไม่มีใครเติมเต็มชิ้นส่วนที่หายไปนี้ได้ ทฤษฎีบทสุดท้ายของเฟอร์มาต์เป็นปัญหาคาใจของเหล่านักคณิตศาสตร์อยู่หลายชั่วอายุคน
เวลาผ่านไปร่วมสามร้อยปี จนในปี 1994 Andrew Wiles ก็สามารถพิสูจน์ทฤษฎีบทสุดท้ายของเฟอร์มาต์ได้ โดยพิจารณาสมการ ด้วยความเป็นกราฟ และเรียกชื่อกราฟนั้นว่า elliptic curve และก็ด้วยเหตุนี้เอง elliptic curve จึงเป็นที่สนใจของบรรดาเหล่านักคณิตศาสตร์ และเป็นกุญแจสำคัญของ Birch and Swinnerton-Dyer Conjectur
คำถามล้านที่ห้านี้ถามว่า ถ้าให้ C เป็น elliptic curve, L(C,s) เป็น L-series ของ C, และ r เป็น rank ของ C บนจำนวนตรรกยะแล้วจะได้ว่า เทอมที่น้อยที่สุดจากการกระจาย L(C,s) ที่ s=1 ก็คือ
Yang-Mills Theory
เป็นความจริงที่ว่าฟิสิกส์ขาดคณิตศาสตร์ไม่ได้ ถ้าไอน์สไตน์พูดแต่เพียงปากเปล่าว่าสสารก็คือพลังงาน และพลังงานก็คือสสาร แต่ไม่สามารถสรุปสมการ ออกมาได้ ทุกวันนี้เราก็อาจจะยังหัวเราะเยาะให้กับความคิดที่ว่าสสารแปลรูปเป็นพลังงานได้
นิวตันรู้ตัวว่างานของเขาต้องการเครื่องมือบางอย่างจากคณิตศาสตร์ ซึ่งเป็นเครื่องมือที่นักคณิตศาสตร์ในยุคนั้นไม่เคยคิดถึง ไม่สนใจ และไม่รู้จัก นิวตันจึงต้องประดิษฐ์เครื่องมือนั้นขึ้นมาเอง เครื่องมือนั้นได้ถูกเรียกว่า "แคลคูลัส" ซึ่งต่อมาก็ได้ถูกโอนเข้าสู่มือนักคณิตศาสตร์ ได้รับการวางรากฐานตามแบบฉบับของคณิตศาสตร์อย่างที่เห็นกันทุกวันนี้
แม้แต่ในยุคนี้สถานการณ์เดิมๆก็ไม่ได้หายไปไหน ปัญหาเกิดขึ้นเมื่อทฤษฎีทางฟิสิกส์ไม่มีทฤษฎีทางคณิตศาสตร์รองรับ
Yang กับ Mills เป็นนักควอนตัมฟิสิกส์ที่ค้นพบปรากฏการณ์บางอย่างจากผลการทดลอง และยืนยันได้จากการจำลองสถานการณ์ด้วยคอมพิวเตอร์ แต่ Yang กับ Mills ไม่สามารถอธิบายสิ่งที่เขาค้นพบได้ด้วยสิ่งที่คณิตศาสตร์มี ไม่สามารถหาสูตรสำเร็จอย่าง ออกมาอธิบายสิ่งที่พวกเขาค้นพบได้
ปัญหาที่มีชื่อว่า Yang-Mills Theory ข้อนี้จึงต่างกับข้ออื่นตรงที่ โจทย์ไม่ได้เป็นคำถามสำเร็จรูปในเชิงคณิตศาสตร์ แต่โจทย์คือการเอาคณิตศาสตร์เข้าไปในที่ที่คณิตศาสตร์ไม่เคยเข้าไป โจทย์ไม่ได้ถามว่าคำตอบของสมการคืออะไร แต่ถามว่าสมการที่นักฟิสิกส์ต้องการคำตอบคือสมการอะไร เหมือนกับที่ไอน์สไตน์พบสูตรพลังงานกับมวลสาร และเหมือนกับที่นิวตันวางรากฐานให้กับวิชาแคลคูลัส
คำถามล้านที่หกก็คือ ให้วางระบบรากฐานในเชิงคณิตศาสตร์ให้เพียงพอ เพื่อที่จะพิสูจน์ได้ว่า Yang-Mills Theory มีจริง และ mass gap (อนุภาคที่มีคุณสมบัติพิเศษอย่างหนึ่งในควอนตัมฟิสิกส์) มีจริง
Hodge Conjecture
ในบรรดาปัญหาทั้งเจ็ด Hodge Conjecture เป็นปัญหาที่เข้าใจยากที่สุดและอธิบายยากที่สุด แต่ทั้งนี้ไม่ได้เป็นเพราะว่า Hodge Conjecture ยากกว่าข้ออื่น แต่ Hodge Conjecture เป็นปัญหาเฉพาะทางที่ลงลึกไปในส่วนของคณิตศาสตร์ที่จินตนาการตามได้ยาก
ภาพ: ด้วยเทคนิคใหม่ๆ นักคณิตศาสตร์สามารถศึกษาและแยกแยะพื้นผิวได้ทุกรูปแบบ
ไอเดียเริ่มต้นก็คือ ถ้าเรานำวัตถุมาทากาวแล้วแปะกันเราก็จะได้รูปทรงใหม่ นักคณิตศาสตร์จึงเริ่มศึกษารูปทรงในหลายมิติที่มาจากการนำรูปทรงที่มีมิติต่ำกว่ามาเชื่อมกัน (ฟังแล้วไม่น่าเชื่อ แต่กระดาษแค่ไม่กี่แผ่นแปะกันก็เกิดเป็นรูปทรงสี่มิติที่ลึกลับซับซ้อนได้ และรูปทรงด้านบนก็เป็นหนึ่งในตัวอย่างที่ได้มาจากวิธีการนี้) เทคนิคดังกล่าวนี้ได้ถูกพัฒนาอย่างแพร่หลายในทุกๆด้าน จนถึงจุดที่วัตถุที่ถูกนำมาเชื่อมติดกันไม่จำเป็นต้องเป็นรูปทรงอีกต่อไป แต่เป็นวัตถุเชิงพีชคณิตที่มีชื่อว่า algebraic cycle วัตถุเชิงพีชคณิตนี้ไม่ได้อยู่ในระบบมิติกว้างยาวสูงที่จับต้องได้ แต่อยู่ในระบบมิติที่มีชื่อว่า projective algebraic variety
คำถามล้านที่เจ็ดถามว่า จริงหรือไม่ ที่บน projective algebraic variety บนจำนวนเชิงซ้อน วัตถุใน Hodge class มาจากจากผสมกันแบบเส้นตรงในเชิงตรรกยะของ algebraic cycle
ถึงแม้ว่า บทพิสูจน์ของ Hodge Conjecture อาจจะไม่ได้เป็นประโยชน์กว้างขวางแบบที่วาดภาพตามได้เหมือนปัญหาข้ออื่นๆ แต่การพัฒนาในสาขาวิชานี้จะเป็นประโยชน์ในวงการอุตสาห์กรรม การออกแบบ และภาพยนตร์แอนิเมชั่น
สมัครสมาชิก:
ความคิดเห็น (Atom)